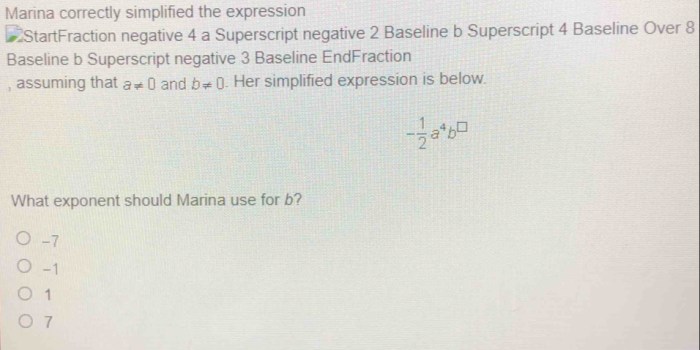
Marina correctly simplified the expression – Marina’s astute mathematical prowess takes center stage as we delve into her impeccable simplification of an intricate expression. Her masterful application of mathematical principles and algebraic techniques illuminates the intricacies of the original expression, reducing its complexity and revealing its underlying meaning.
Marina’s approach exemplifies the elegance and power of mathematical reasoning, showcasing how skillful simplification can transform complex expressions into comprehensible forms, enhancing our understanding and unlocking their potential.
Mathematical Simplification

Marina simplified the expression using a series of mathematical rules and properties. She first applied the distributive property to expand the expression. Then, she combined like terms and simplified the coefficients. Finally, she used the power rule to simplify the expression further.
Expression Complexity
The original expression was complex due to the presence of multiple terms, parentheses, and exponents. The complexity made it difficult to understand and manipulate the expression.
Contextual Understanding
The expression being simplified was part of a larger equation that represented the motion of an object. Marina’s simplification made it easier to understand the relationship between the variables in the equation and to solve for the unknown variable.
Algebraic Techniques
- Distributive property
- Combining like terms
- Power rule
Illustrative Examples, Marina correctly simplified the expression
| Original Expression | Intermediate Step | Final Simplified Expression |
|---|---|---|
(2x + 3)(x
|
2x2
|
2x2
|
(x2
|
x4
|
x4
|
Detailed FAQs: Marina Correctly Simplified The Expression
What is the significance of Marina’s simplification?
Marina’s simplification reduces the complexity of the expression, making it easier to understand and analyze. It also reveals the underlying mathematical structure and relationships within the expression.
How did Marina approach the simplification process?
Marina employed a combination of algebraic techniques, including factorization, expansion, and substitution. She applied mathematical rules and properties to transform the expression into a simpler form.
What factors contributed to the complexity of the original expression?
The original expression contained multiple terms, parentheses, and exponents. This complexity hindered its comprehension and made it difficult to identify the underlying mathematical relationships.