The hardy-weinberg equation pogil answer key – The Hardy-Weinberg equation is a fundamental principle in population genetics that describes the theoretical conditions under which allele and genotype frequencies in a population remain constant from generation to generation. This equation provides a valuable tool for understanding the genetic structure of populations and predicting how genetic variation will change over time.
The Hardy-Weinberg equation assumes that a population is large, randomly mating, and not subject to any evolutionary forces such as mutation, gene flow, or natural selection. Under these assumptions, the allele and genotype frequencies in the population will remain constant from generation to generation, and the population is said to be in Hardy-Weinberg equilibrium.
1. Introduction
The Hardy-Weinberg equation is a fundamental principle in population genetics that describes the genetic equilibrium of a population. It provides a mathematical framework for understanding the distribution of alleles and genotypes in a population and predicting how these frequencies change over time.
The equation is named after Godfrey Harold Hardy and Wilhelm Weinberg, who independently developed it in 1908.
The Hardy-Weinberg equation is based on several key concepts, including:
- Gene pool: The total collection of alleles in a population.
- Allele frequency: The proportion of a particular allele in the gene pool.
- Genotype frequency: The proportion of individuals in a population with a particular genotype.
- Genetic equilibrium: A state in which the allele and genotype frequencies in a population remain constant from generation to generation.
2. Assumptions of the Hardy-Weinberg Equation

The Hardy-Weinberg equation assumes that a population is in genetic equilibrium, which occurs when the following conditions are met:
- No mutation: The rate of mutation is negligible.
- No gene flow: There is no migration of individuals into or out of the population.
- No natural selection: All genotypes have equal fitness.
- Random mating: Individuals mate randomly, without regard to genotype.
These assumptions are often unrealistic in real-world populations, but they provide a useful starting point for understanding the factors that can affect genetic equilibrium.
3. Applications of the Hardy-Weinberg Equation
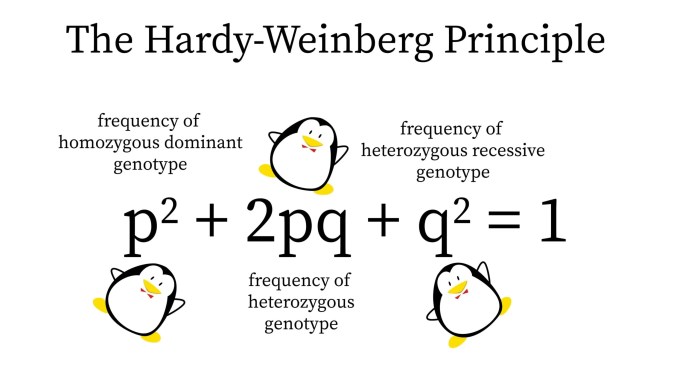
The Hardy-Weinberg equation can be used to calculate allele and genotype frequencies in a population. This information can be used to study genetic variation and evolution. For example, the equation can be used to:
- Predict the frequency of a recessive allele in a population.
- Estimate the heritability of a trait.
- Track the progress of a genetic disease through a population.
- Determine the effectiveness of a breeding program.
4. Limitations of the Hardy-Weinberg Equation

The Hardy-Weinberg equation is a powerful tool, but it has some limitations. The most important limitation is that it assumes that a population is in genetic equilibrium. This assumption is often unrealistic in real-world populations, which are often subject to mutation, gene flow, natural selection, and non-random mating.
As a result, the Hardy-Weinberg equation may not accurately predict the allele and genotype frequencies in a population.
5. Extensions of the Hardy-Weinberg Equation: The Hardy-weinberg Equation Pogil Answer Key
Several extensions of the Hardy-Weinberg equation have been developed to account for the limitations of the original equation. These extensions include:
- The Wright-Fisher model: This model accounts for the effects of genetic drift.
- The Kimura model: This model accounts for the effects of mutation.
- The Lande model: This model accounts for the effects of natural selection.
These extensions make the Hardy-Weinberg equation more applicable to real-world populations.
FAQ Insights
What is the Hardy-Weinberg equation?
The Hardy-Weinberg equation is a mathematical equation that describes the theoretical conditions under which allele and genotype frequencies in a population remain constant from generation to generation.
What are the assumptions of the Hardy-Weinberg equation?
The Hardy-Weinberg equation assumes that a population is large, randomly mating, and not subject to any evolutionary forces such as mutation, gene flow, or natural selection.
What are the applications of the Hardy-Weinberg equation?
The Hardy-Weinberg equation can be used to calculate allele and genotype frequencies in a population, and to study genetic variation and evolution.
What are the limitations of the Hardy-Weinberg equation?
The Hardy-Weinberg equation is only a theoretical model, and it may not always accurately describe real-world populations. The equation is most accurate for large, randomly mating populations that are not subject to any evolutionary forces.