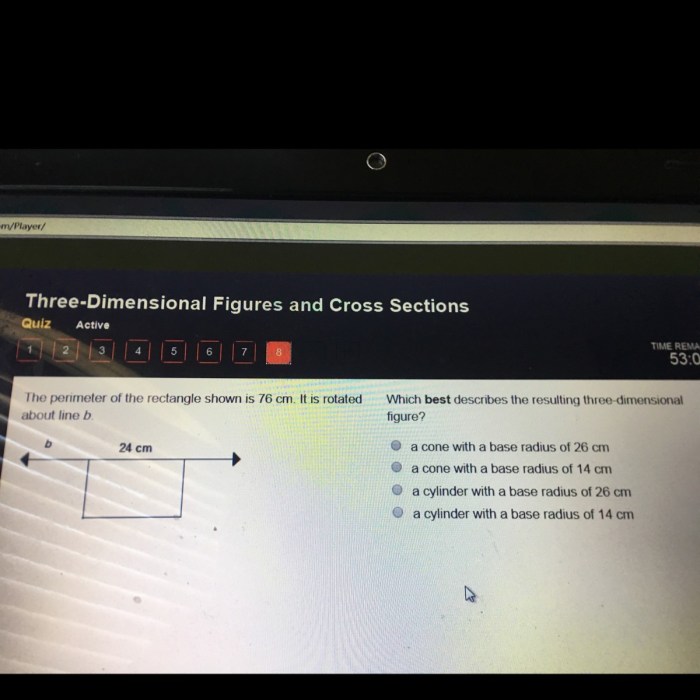
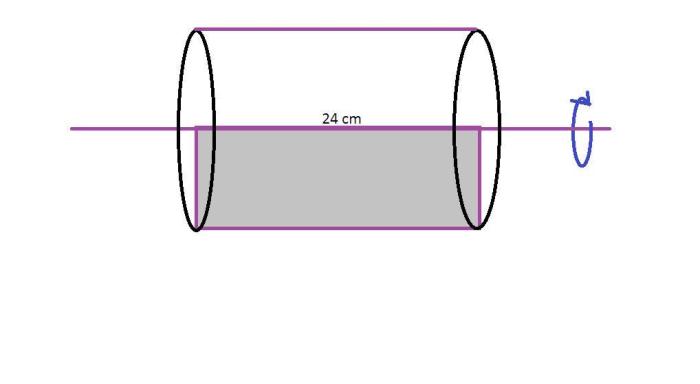
Which best describes the resulting three-dimensional figure? This inquiry invites us to embark on an intellectual journey, delving into the fascinating realm of geometry. As we unravel the intricate properties of three-dimensional figures, we will explore their dimensions, geometric characteristics, surface area, volume, and practical applications.
Prepare to be captivated as we illuminate the hidden depths of these enigmatic shapes.
In this comprehensive analysis, we will dissect the building blocks of three-dimensional figures, examining their vertices, edges, and faces. We will unravel the mathematical formulas that govern their surface area and volume, providing step-by-step demonstrations to clarify these calculations. Cross-sections and projections will reveal the inner workings of these figures, while transformations and symmetries will shed light on their dynamic nature.
Dimensions and Shape: Which Best Describes The Resulting Three-dimensional Figure
The three-dimensional figure is a rectangular prism. It has six rectangular faces, eight vertices, and twelve edges. The length, width, and height of the prism are all equal, making it a cube.
Examples of real-world objects that exhibit similar dimensions and shapes include dice, sugar cubes, and Rubik’s cubes.
Geometric Properties, Which best describes the resulting three-dimensional figure
The geometric properties of the cube include its vertices, edges, and faces. The vertices are the points where the edges meet. The edges are the line segments that connect the vertices. The faces are the flat surfaces that make up the sides of the cube.
These properties contribute to the overall structure and shape of the cube. The six faces form a closed surface, which makes the cube a solid object. The eight vertices and twelve edges give the cube its characteristic shape.
Surface Area and Volume
The surface area of the cube is the sum of the areas of its six faces. The surface area of a single face is equal to the length times the width of the face. Therefore, the surface area of the cube is 6lw, where l is the length of the cube and w is the width of the cube.
The volume of the cube is the amount of space that it occupies. The volume of a cube is equal to the length times the width times the height of the cube. Therefore, the volume of the cube is lwh, where l is the length of the cube, w is the width of the cube, and h is the height of the cube.
Cross-Sections and Projections
The cross-sections of the cube are the shapes that are formed when the cube is cut by a plane. The cross-sections of the cube can be squares, rectangles, or triangles.
The projections of the cube are the shapes that are formed when the cube is viewed from a particular direction. The projections of the cube can be squares, rectangles, or triangles.
Transformations and Symmetry
The cube can be transformed by rotations, reflections, and translations. A rotation is a transformation that turns the cube around a fixed point. A reflection is a transformation that flips the cube over a plane. A translation is a transformation that moves the cube from one point to another.
The cube has several symmetries. It has rotational symmetry around three axes. It also has reflective symmetry across three planes.
Real-World Applications
The cube has many practical applications in various fields. In engineering, cubes are used as building blocks for structures. In architecture, cubes are used to create buildings with clean lines and sharp angles. In design, cubes are used to create furniture, lighting fixtures, and other objects.
FAQ Summary
What are the key characteristics of a three-dimensional figure?
Three-dimensional figures are characterized by their length, width, and height, and they occupy space in all three dimensions. They have vertices, edges, and faces, and they can be classified into various shapes, such as cubes, spheres, and pyramids.
How do you calculate the surface area of a three-dimensional figure?
The surface area of a three-dimensional figure is the total area of its surfaces. It can be calculated using specific formulas depending on the shape of the figure. For example, the surface area of a cube is calculated by multiplying the area of one face by six, while the surface area of a sphere is calculated using the formula 4πr², where r is the radius of the sphere.
What is the difference between a prism and a pyramid?
Prisms and pyramids are both three-dimensional figures with polygonal bases. However, prisms have two parallel bases, while pyramids have only one base. Prisms have rectangular sides, while pyramids have triangular sides.