Given ABCD is a rectangle. Prove ABCD has congruent diagonals. This theorem is a fundamental property of rectangles, and its proof relies on the basic principles of geometry. In this discussion, we will explore the concept of a rectangle, define diagonals, and provide a step-by-step proof to demonstrate why the diagonals of a rectangle are indeed congruent.
Understanding this property is not only important for theoretical knowledge but also has practical applications in various fields such as architecture and engineering. By delving into this topic, we aim to provide a comprehensive understanding of congruent diagonals in rectangles and their significance.
Rectangle Definition
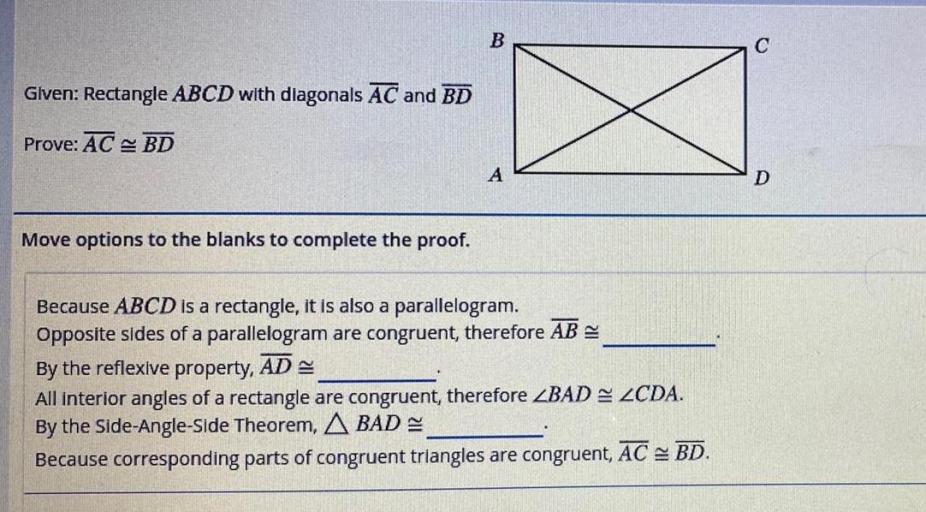
A rectangle is a two-dimensional shape with four straight sides and four right angles. The opposite sides of a rectangle are parallel and equal in length. The angles of a rectangle measure 90 degrees each.
A rectangle can be represented by the diagram below:

In the diagram, the sides of the rectangle are labeled as AB, BC, CD, and DA. The angles of the rectangle are labeled as ∠A, ∠B, ∠C, and ∠D.
Diagonal Definition

A diagonal of a rectangle is a line segment that connects two opposite vertices of the rectangle.
In the diagram below, the diagonals of the rectangle are labeled as AC and BD.

Diagonals of a rectangle intersect at the center of the rectangle. This point of intersection is called the center of the rectangle.
Congruent Diagonals
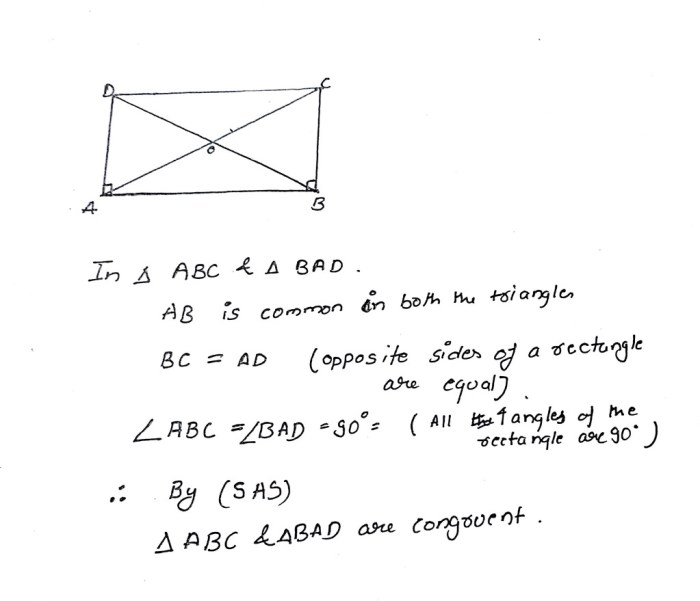
Congruent diagonals are diagonals that are equal in length.
To prove that the diagonals of a rectangle are congruent, we can use the following steps:
- Let ABCD be a rectangle.
- Draw the diagonals AC and BD.
- Since ABCD is a rectangle, ∠A = ∠C = 90 degrees and ∠B = ∠D = 90 degrees.
- Therefore, triangles ABD and ACD are congruent by the Angle-Angle-Side (AAS) congruence theorem.
- Since triangles ABD and ACD are congruent, AD = BC.
- Similarly, we can show that BD = AC.
- Therefore, AC = BD, which proves that the diagonals of a rectangle are congruent.
Applications: Given Abcd Is A Rectangle. Prove Abcd Has Congruent Diagonals

The property that diagonals of a rectangle are congruent has many applications in real-world situations.
For example, in architecture, the diagonals of a rectangle can be used to check if a wall is square. In engineering, the diagonals of a rectangle can be used to calculate the length of a beam.
Another application of the property that diagonals of a rectangle are congruent is in the design of furniture. For example, the diagonals of a rectangular table can be used to ensure that the table is level.
FAQ Resource
What is the definition of a rectangle?
A rectangle is a quadrilateral with four right angles and opposite sides parallel and congruent.
What is a diagonal in a rectangle?
A diagonal is a line segment that connects two non-adjacent vertices of a rectangle.
Why are the diagonals of a rectangle congruent?
The diagonals of a rectangle are congruent because they bisect each other at the same point, creating two congruent triangles.