The electric flux through the shaded surface is a fundamental concept in electromagnetism that quantifies the amount of electric field passing through a given area. This concept plays a pivotal role in analyzing electric fields, understanding Gauss’s law, and solving complex problems in electrostatics, capacitors, and antennas.
In this comprehensive exploration, we will delve into the intricacies of electric flux, examining its mathematical formulation, applications in various fields, and the use of symmetry and numerical methods to simplify its calculation.
The Concept of Electric Flux
Electric flux is a measure of the amount of electric field passing through a given surface. It is defined as the total electric field passing through the surface, weighted by the cosine of the angle between the electric field and the normal to the surface.
Electric flux is an important concept in electromagnetism, as it can be used to analyze electric fields and determine the charge distribution within a region.
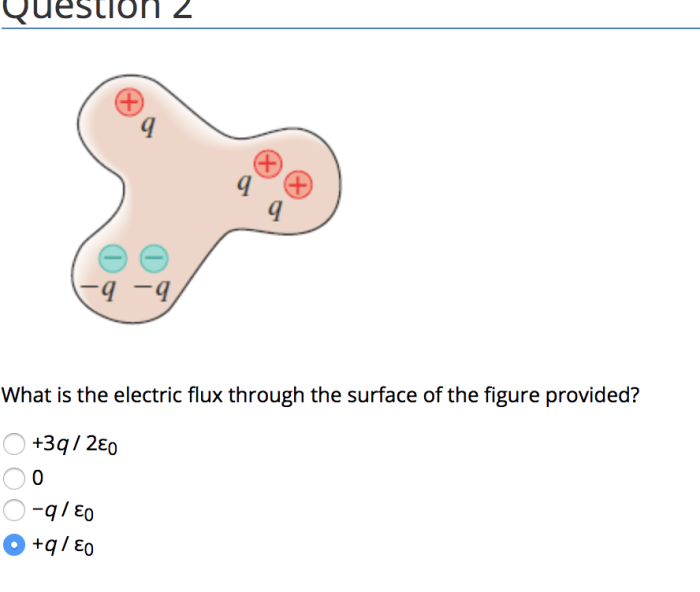
Electric flux is often used to analyze the electric field around conductors and insulators. For example, the electric flux through a closed surface surrounding a conductor is equal to the net charge enclosed by the surface. This result is known as Gauss’s law and is one of the most important laws in electromagnetism.
Calculating Electric Flux through a Surface: The Electric Flux Through The Shaded Surface Is
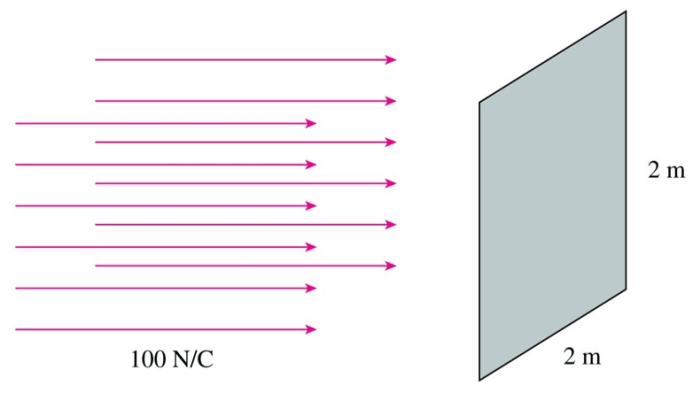
The electric flux through a surface can be calculated using the following formula:
$$\Phi_e = \int\int \overrightarrowE \cdot \hatn dA$$
where:
- $\overrightarrowE$ is the electric field vector
- $\hatn$ is the unit normal vector to the surface
- $dA$ is the differential surface area
The integral is evaluated over the entire surface.
In practice, it is often convenient to use a differential surface element to calculate the electric flux. A differential surface element is a small, flat surface that is perpendicular to the electric field vector. The electric flux through a differential surface element is given by:
$$\Delta\Phi_e = E dA \cos\theta$$
where $\theta$ is the angle between the electric field vector and the normal to the surface element.
Applications of Electric Flux
Electric flux has a wide range of applications in electrostatics, capacitors, and antennas. In electrostatics, electric flux can be used to determine the electric field distribution around conductors and insulators. In capacitors, electric flux can be used to calculate the capacitance of the capacitor.
In antennas, electric flux can be used to calculate the radiation pattern of the antenna.
One important application of electric flux is in the design of capacitors. A capacitor is a device that stores electrical energy in an electric field. The capacitance of a capacitor is determined by the amount of electric flux that can be stored in the capacitor.
The greater the electric flux, the greater the capacitance.
Electric Flux and Symmetry
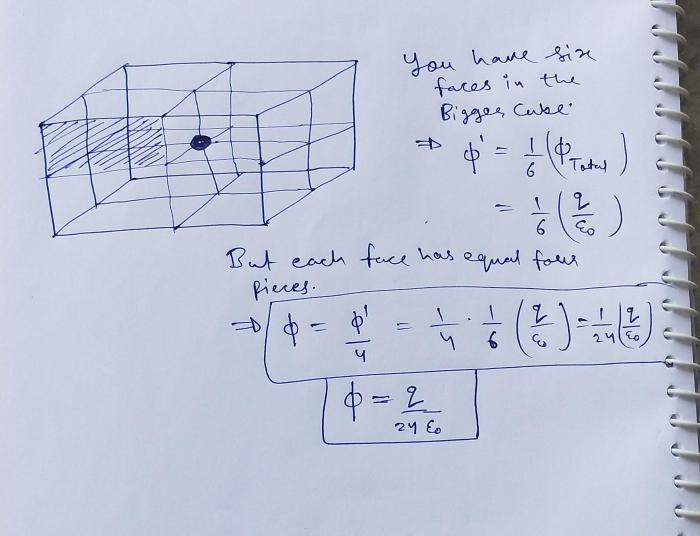
Symmetry can be used to simplify electric flux calculations. For example, if a charge distribution has spherical symmetry, then the electric field around the charge distribution will also have spherical symmetry. This means that the electric flux through any spherical surface surrounding the charge distribution will be the same.
Gauss’s law can be used to determine the electric flux for symmetric charge distributions. For example, the electric flux through a spherical surface surrounding a point charge is given by:
$$\Phi_e = \fracQ\epsilon_0$$
where Q is the charge enclosed by the surface and $\epsilon_0$ is the permittivity of free space.
Electric Flux in Different Media
The permittivity of a material affects the electric flux passing through it. The permittivity of a material is a measure of how easily the material can be polarized by an electric field. The greater the permittivity, the more easily the material can be polarized and the greater the electric flux that will pass through the material.
For example, the permittivity of free space is approximately 8.85 x 10^-12 F/m. The permittivity of water is approximately 80 x 10^-12 F/m. This means that electric flux will pass through water more easily than it will pass through free space.
Visualizing Electric Flux
Electric flux lines are a useful tool for visualizing the electric field. Electric flux lines are lines that are drawn in the direction of the electric field vector. The density of the flux lines is proportional to the magnitude of the electric field vector.
Electric flux lines can be used to understand the direction and magnitude of electric fields. For example, the electric flux lines around a point charge are radial. This means that the electric field vector points away from the point charge in all directions.
Numerical Methods for Electric Flux Calculations
Numerical methods can be used to calculate electric flux for complex geometries. One common numerical method is the finite element method (FEM). FEM is a technique for dividing a complex geometry into a number of smaller, simpler elements. The electric flux through each element is then calculated using the appropriate formula.
The total electric flux through the entire geometry is then found by summing the electric flux through each element.
FEM is a powerful tool for calculating electric flux for complex geometries. It is used in a wide range of applications, including the design of capacitors, antennas, and other electrical devices.
Helpful Answers
What is the significance of electric flux?
Electric flux provides a measure of the total electric field passing through a given surface, aiding in the analysis and understanding of electric field distributions.
How is electric flux related to Gauss’s law?
Gauss’s law establishes a direct relationship between the electric flux through a closed surface and the enclosed electric charge, providing a powerful tool for calculating electric fields.
What are the applications of electric flux?
Electric flux finds applications in electrostatics, capacitors, antennas, and various other fields, enabling the determination of electric field distributions and the analysis of electrical systems.