The Stretching and Shrinking Answer Key serves as a definitive guide to understanding the concepts, transformations, and applications of stretching and shrinking in geometry and beyond. This comprehensive resource unravels the intricacies of these transformations, providing a clear and concise overview for students, researchers, and professionals alike.

Stretching and shrinking are fundamental geometric operations that involve manipulating the size and shape of objects. They play a crucial role in various fields, including computer graphics, engineering, and biology. This answer key provides a deep dive into the mathematical principles, types, matrix representations, and applications of these transformations.

Stretching and Shrinking

In geometry, stretching and shrinking refer to the transformation of a geometric figure by either enlarging or reducing its size while maintaining its shape.

Stretching involves increasing the size of a figure, while shrinking involves decreasing its size. These transformations can be applied in various real-world scenarios, such as:

• Enlarging a blueprint to create a full-scale model
• Shrinking a map to fit a smaller space
• Enlarging or shrinking an image to fit a specific display size

Mathematically, stretching and shrinking are achieved by multiplying the coordinates of the original figure by a constant factor. This factor, known as the scale factor, determines the amount of enlargement or reduction.

Types of Stretching and Shrinking

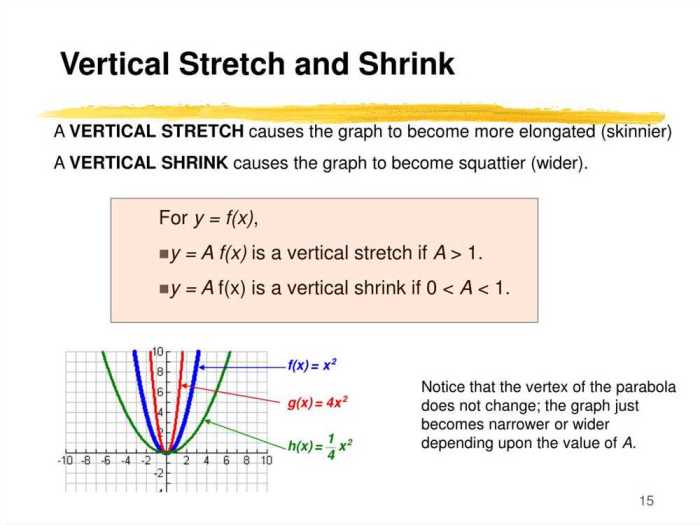
Stretching and shrinking transformations are mathematical operations that alter the size and shape of a figure. There are three main types of stretching and shrinking transformations: uniform stretching, non-uniform stretching, and shrinking.

Uniform Stretching

Uniform stretching is a transformation that increases or decreases the size of a figure by the same factor in all directions. This means that the shape of the figure remains the same, but its size changes. Uniform stretching is also known as isotropic scaling.

The following image shows an example of uniform stretching. The original figure (in blue) has been stretched by a factor of 2 in all directions. The resulting figure (in red) is twice as large as the original figure, but it has the same shape.

[Image of a square being stretched by a factor of 2 in all directions]

Non-uniform Stretching

Non-uniform stretching is a transformation that increases or decreases the size of a figure by different factors in different directions. This means that the shape of the figure changes. Non-uniform stretching is also known as anisotropic scaling.

The following image shows an example of non-uniform stretching. The original figure (in blue) has been stretched by a factor of 2 in the x-direction and by a factor of 3 in the y-direction. The resulting figure (in red) is taller and narrower than the original figure.

[Image of a rectangle being stretched by a factor of 2 in the x-direction and by a factor of 3 in the y-direction]

Shrinking

Shrinking is a transformation that decreases the size of a figure. Shrinking is the opposite of stretching. The following image shows an example of shrinking. The original figure (in blue) has been shrunk by a factor of 2 in all directions.

The resulting figure (in red) is half the size of the original figure.

[Image of a square being shrunk by a factor of 2 in all directions]

Matrix Representation of Stretching and Shrinking

Stretching and shrinking transformations can be conveniently represented using matrices. A transformation matrix is a square matrix that encodes the transformation’s parameters, allowing for easy manipulation and application to vectors and points.

To construct the matrix for a given stretching or shrinking transformation, follow these steps:

1. Identify the scaling factors for each coordinate axis. Let s_xand s_yrepresent the scaling factors for the xand yaxes, respectively.
2. Construct a diagonal matrix with the scaling factors on the diagonal:

$$S = \beginbmatrix s_x & 0 \\\ 0 & s_y \endbmatrix$$

3. If the transformation involves a translation or rotation, construct a translation or rotation matrix and multiply it with the scaling matrix S.

The resulting matrix represents the combined transformation. Applying this matrix to a vector or point will perform the specified stretching, shrinking, translation, or rotation.

Transformation matrices have several useful properties:

• The identity matrix, which has 1s on the diagonal and 0s elsewhere, represents no transformation.
• The inverse of a transformation matrix represents the inverse transformation.
• Concatenating transformation matrices represents the combined transformation.

These properties make transformation matrices a powerful tool for manipulating and analyzing geometric transformations.

Applications of Stretching and Shrinking in Computer Graphics

Stretching and shrinking are fundamental transformations in computer graphics, used extensively for scaling, resizing, and creating perspective effects. These transformations manipulate the size and shape of objects, allowing for realistic and visually appealing graphics.

Scaling and Resizing

Scaling and resizing involve uniformly increasing or decreasing the size of an object. Scaling factors are applied to the object’s dimensions, resulting in a proportional change in size. This transformation is crucial for resizing images, adjusting the size of objects within a scene, and maintaining aspect ratios.

Perspective Transformations

Perspective transformations create the illusion of depth and distance in 3D graphics. By applying a perspective matrix to an object, its size and shape are distorted to simulate the effects of perspective. This transformation is essential for creating realistic scenes, simulating camera movements, and providing a sense of spatial awareness.

In graphics software, stretching and shrinking transformations are typically implemented using matrix operations. Transformation matrices are applied to the object’s vertices, altering their positions and creating the desired effect. These transformations can be combined and applied sequentially to achieve complex deformations.

Importance in Computer Graphics

Stretching and shrinking are vital in computer graphics for several reasons:

• Adaptability:They allow objects to be scaled and resized to fit different screen resolutions, aspect ratios, and scene requirements.
• Perspective Control:Perspective transformations create depth and realism, enhancing the immersion and visual appeal of 3D graphics.
• Object Manipulation:Stretching and shrinking enable dynamic manipulation of objects within a scene, allowing for animation, deformation, and shape changes.
• Image Processing:These transformations are used in image processing applications, such as resizing, cropping, and adjusting aspect ratios.

Applications of Stretching and Shrinking in Other Fields: Stretching And Shrinking Answer Key

Beyond geometry and computer graphics, stretching and shrinking transformations find widespread applications in diverse scientific and engineering disciplines. These transformations enable the manipulation of objects and data to gain insights, solve problems, and optimize designs.

In physics, stretching and shrinking play a crucial role in understanding the behavior of elastic materials. The concept of elasticity describes how objects deform under applied forces and return to their original shape when the forces are removed. The stretching and shrinking of elastic materials can be analyzed using mathematical models that incorporate these transformations.

Engineering Applications

In engineering, stretching and shrinking transformations are employed in various fields, including:

• Structural Engineering:Stretching and shrinking transformations are used to analyze the behavior of structures under different loading conditions. These transformations help engineers predict how structures will deform and withstand forces, ensuring their safety and stability.
• Mechanical Engineering:In the design of mechanical systems, stretching and shrinking transformations are used to analyze the deformation of components under various operating conditions. This knowledge helps engineers optimize the design of components to prevent failure and ensure efficient operation.
• Materials Science:Stretching and shrinking transformations are used to study the properties of materials under different stress conditions. These transformations provide insights into the material’s elasticity, strength, and toughness, aiding in the development of new materials with desired properties.

Biology Applications, Stretching and shrinking answer key

In biology, stretching and shrinking transformations have significant applications in:

• Biomechanics:Stretching and shrinking transformations are used to analyze the movement and deformation of biological structures, such as muscles, tendons, and bones. These transformations help researchers understand the mechanics of biological systems and develop treatments for musculoskeletal disorders.
• Cell Biology:Stretching and shrinking transformations are used to study the behavior of cells under different mechanical forces. These transformations provide insights into cell migration, adhesion, and differentiation, contributing to the understanding of cellular processes and the development of therapies for diseases.

• Developmental Biology:Stretching and shrinking transformations are used to model the growth and development of biological structures. These transformations help researchers understand the mechanisms that control tissue formation and organogenesis.

Essential Questionnaire

What is the difference between uniform and non-uniform stretching?

Uniform stretching scales an object equally in all directions, while non-uniform stretching scales an object differently in different directions.

How are stretching and shrinking transformations represented using matrices?

Stretching and shrinking transformations can be represented using 2×2 or 3×3 matrices, depending on the dimension of the transformation.

What are some applications of stretching and shrinking in computer graphics?

Stretching and shrinking are used in computer graphics for scaling, resizing, and perspective transformations.